+62 21 54376065

Mekanik pada sistem Variable Speed Drive (VSD)

Seri 2

1.5    Energi

Pada gerak translasi kita mengenal usaha yang didefinisikan sebagai gayayang dibutuhkan untuk mengerakkan suatu benda sejauh (lihat gambar 2 pada seri 1).

Didalam rumus dinyatakan sebagai berikut:

Satuan usaha adalah Nm atau J (Joule).

Usaha yang tersimpan disebut energi.

Ada bermacam macam energi dalam kehidupan sehari hari, antara lain:

energi untuk mengangkat, energi untuk mengaselerasi, energi untuk mengecas pegas,energi  gesekan, energi  panas, energi  bunyi, energi cahaya, energy nuklir, energi  matahari, energi  angin, energi  air  dan lain lain.

Ada 2 jenis energi, yaitu energi potensial dan energi kinetik.

1.5.1  Energi Potensial

Energi potensial adalah energi yang tersimpan pada obyek karena kondisi atau posisinya.

Contoh energi potensial  adalah:

·         Energi gravitasi 

·         Energi yang tersimpan didalam pegas  

·         Energi medan listrik 

·         Energi medan magnet pada induktor     

·         Energi  yang tersimpan didalam kapasitor 

·         Energi pada batere 

·         Energi Listrik   

·         dan lain lain

1.5.2  Energi Kinetik Translasi

Energi potensial mempunyai potensi untuk dirubah menjadi energi kinetik.

Dalam hal ini energi listrik termasuk energi potensial .

Energi kinetik adalah energi dari massa yang  bergerak.

Untuk gerak translasi berlaku:

1.5.3  Energi Kinetik Rotasi

Rotasi adalah perputaran suatu obyek mengelilingi sumbu putarnya.

Pada rotasi tidak menyebabkan terjadi translasi.

Benda yang berotasi memiliki energi kinetik.

dengan:

Untuk benda yang berotasi dari diam ke kecepatan sudut tertentu dengan percepatan sudut  berlaku:

Sehingga  energi kinetik dari benda yang berotasi adalah:

Dengan substitusikan   ke persamaan diatas, maka kita peroleh energi kinetik rotasi:

Persamaan ini mempunyai kesamaan dengan energi  kinetik dari benda yang bertranslasi, yaitu:

·         massa dari gerak translasi identik dengan momen kelembaman dari gerak rotasi

·         kecepatan linear pada gerak translasi identik dengan kecepatan sudut pada gerak rotasi

Kesimpulan:

Didalam suatu sistem tertutup berlaku hukum kekekalan energi, yaitu:

Energi  tidak dapat di ciptakan maupun dimusnahkan, energi hanya dapat dirubah dari satu bentuk ke bentuk yang lain.

Sehingga didalam satu sistem tertutup jumlah semua energi potensial dan energi kinetik (baik translasi maupun rotasi) adalah konstan.

1.6      Momen Kelembaman atau Inersia

Momen Kelembaman atau Inersia adalah resistansi dari suatu objek yang bergerak melawan percepatan (atau perlambatan) atau dengan kata lain keegganan untuk merespons perubahan gerak.

Dalam kehidupan sehari hari kita jumpai, umpamanya sewaktu kita mengerem kenderaan yang lagi melaju cepat. Walaupun kita sudah mengerem, kenderaan kita masih akan terus melaju selama beberapa saat lamanya sebelum berhenti  sama sekali.

Gambar 15: Inersia

dengan:

Torsi total oleh momen kelembaman yang terbentuk merupakan jumlah (Integral) dari elemen elemen massa menjadi:

 sebagai Momen Kelembaman atau Inersia  dengan dimensi  , dimana:

maka:

Momen kelembaman suatu benda padat selain tergantung dari massa (yang merupakan kumpulan dari elemen elemen massa yang membentuk benda padat tersebut) yang bergerak juga tergantung dari bentuknya. Selain itu momen kelembaman  juga tergantung arah dari sumbu putarnya.

Inersia suatu benda padat yang tidak beraturan dapat dihitung dengan membiarkan benda tersebut diputar terhadap suatu sumbu yang melewati pusat massa benda itu.

Untuk menghitung inersia benda benda yang bergeser sumbu putar nya terhadap titik berat seperti yang dilukiskan pada gambar 16, dapat dipakai hukum Steiner.

Gambar 16: Pergeseran sumbu putar sejauh  a  terhadap titik berat

Jika pergeseran sumbu putar sejauh a terhadap sumbu putar yang melalui titik berat (x-x), maka momen kelembaman menjadi:

1.6.1  Momen Kelembaman dari Silinder Pejal

Gambar 17: Silinder pejal

dengan:

dengan: 

dimana:

Dengan memakai hukum Steiner kita dapat menghitung momen kelembaman siatu silinder pejal yang sumbu putarnya bergeser sejauh r sumbu putar yang melaui titik beratnya (x-x).

Gambar 18: Sumbu putar bergeser r dari titik berat

Dengan mengapplikasikan hukum Steiner dengan pergeseran a =r, maka:

1.6.2  Momen Kelembaman untuk silinder dengan dinding yang tipis

Gambar 19: Silinder dengan Dinding Tipis

sehingga:

Volume silinder kosong adalah:
 

Sehingga massa silinder kosong menjadi:

Dengan mensubsitusikan: 

1.6.3  Momen Kelembaman dari beberapa benda

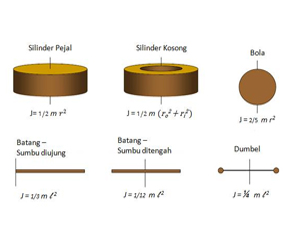
Beberapa bentuk geometri tertentu yang sering dipakai sudah langsung dapat diambil dari buku tabel  tanpa harus melakukan perhitungan seperti diatas.

Pada gambar 20 dibawah diperlihatkan geometri tertentu dengan momen kelembamannya masing masing.

Gambar 20: Momen kelembaman  dari beberapa geometri